Архаичные шифраторы канули в Лету, чего нельзя сказать об алгоритмах шифрования. Операции сдвига, замены и перестановки до сих пор применяются в современных алгоритмах, однако с существенной поправкой в стойкости. За многие столетия, прошедшие со времен первого применения этих шифров, криптографы научились оценивать количество информации, энтропию и стойкость, однако так было не всегда. Рассмотрим подробнее, как работают самые популярные шифры в истории криптографии и в чем их недостатки.

В современном обществе, где почти каждый человек имеет электронный девайс (а то и не один), где каждую минуту совершаются операции с электронной валютой, пересылаются конфиденциальные email, подписываются электронные документы, криптография нужна как воздух. Нужна пользователям, чтобы защитить свою приватность. Нужна программистам, чтобы обеспечить безопасность проектируемых систем. Нужна хакерам, чтобы при аудите понимать уязвимые места в системах. Нужна админам, чтобы представлять, чем и как лучше защищать корпоративные данные. Мы не могли обойти стороной такую важную тему и начинаем цикл статей, посвященный введению в криптoграфию. Для новичков — самый простой путь познакомиться с криптой, для профи — хороший повод систематизировать свои знания. Шесть уроков, от самого простого к сложному. Вперед!
Термины
Для начала давай определимся с терминологией:
- Криптография — это наука о том, как обеспечить секретность сообщения.
- Криптоанализ — это наука о том, как вскрыть зашифрованное сообщение, не зная ключа.
- Дешифровка — это процeсс получения открытого текста средствами криптоанализа.
- Расшифрование — это процесс получения открытого текста с использованием ключа и алгоритма расшифрования, предусмотренного для данного шифра.
В мире криптографии путаться в этих словах — ужасный моветон.
Зачем мне знания о криптографии?
Предположим, криптография очень нужна, но пусть ей займутся дядьки с усами математики. Зачем же мне знания по криптографии?
Если ты обычный пользователь — то как минимум, чтобы обеспечить свою приватность. Сегодня крупным государствам и влиятельным организациям становятся доступны средства тотального надзора за миллионами людей. Поэтому криптография оказывается важнейшим инструментом, обеспечивающим конфиденциальность, доверие, целостность, авторизацию сообщений и электронных платежей. Повсеместное распространение криптографии останется одним из немногих способов защитить пользователя от угроз, нависающих над его конфиденциальной информацией. Зная, как работает тот или иной протокол или шифр, чем он хорош и где его слабые места, ты сможешь оcознанно выбирать инструменты для работы или просто общения в Сети.
Если ты программист или специалист по ИБ, то здесь вообще от криптографии никуда не скрыться. Любой крупный проект требует обеспечения безопасности информации. Неважно, что ты разрабатываешь: контентный сервис, почтовик, мессенджер, соцсеть или просто интернет-магазин, — везде есть критичные данные, которые надо защищать от перехвата или угона БД. Каждая операция должна быть защищена криптографическими протоколами. В этом случае криптография — подходящий инструмент. Если ты еще с ней не столкнулся, будь уверен — это на 100% лишь вопрос времени.
Короче говоря, криптография используется гораздо чаще, чем можно себе представить. Поэтому пора снять завесу тайны с этой науки, познакомиться с наиболее интересными аспектами и использовать ее возможности себе на пользу.
Зачем изучать старые шифры?
В интернете криптографические протоколы используются практически при каждом запросе. Но как же дело обстояло, когда интернета не было и в помине? Не стоит думать, что в те далекие лохматые времена не было криптографии. Первые способы шифрования появились около четырех тысяч лет назад. Конечно, это были самые примитивные и нестойкие шифры, однако и население тогда было малограмотное, так что такие способы могли защитить информацию от любопытных глаз.
Люди всегда нуждались в секретной переписке, поэтому шифрование не стояло на месте. С раскрытием одних шифров придумывали другие, более стойкие. На смену бумажным шифрам пришли шифровальные машины, которым не было равных среди людей. Даже опытному математику не удавалось взломать шифр, рассчитанный на роторной машине. С появлением первых компьютеров требования к защите информации возросли многократно.
Зачем же нам знакомиться с такими древними и нестойкими шифрами, если можно сразу прочитать про DES и RSA — и вуаля, почти специалист? Изучение первых шифров поможет лучше понять, зачем нужна та или иная операция в современном алгоритме шифрования. Например, шифр перестановки, один из первых примитивных алгоритмов, не был забыт, и перестановка — одна из часто встречающихся операций в современном шифровании. Таким образом, чтобы лучше осознать, откуда на самом деле растут ноги у современных алгоритмов, нужно оглянуться на несколько тысяч лет назад.
Исторические шифры и первые шифраторы
Согласно источникам, первые способы шифрования текста появились вместе с зарождением письменности. Способы тайного письма применялись древними цивилизациями Индии, Месопотамии и Египта. В письменах Древней Индии упоминаются способы изменения текста, которые использовали не только правители, но и ремесленники, желающие скрыть секрет мастерства. Истоком криптографии считается использование специальных иероглифов в древнеегипетской письменности около четырех тысячелетий назад.
Первым шифром, зародившимся в древних цивилизациях и актуальным, в некотором роде, и по сей день, можно считать шифр замены. Чуть позже был придуман шифр сдвига, который применялся Юлием Цезарем, почему и был назван в его честь.
Помимо шифров, нельзя не упомянуть о приборах для шифрования, которые разрабатывали древние математики. Например, скитала — первый шифратор, разработанный в Спарте. Представлял собой палку, на которую по всей длине наматывалась лента пергамента. Текст наносился вдоль оси палки, после чего пергамент снимался, и получалось шифрованное сообщение. Ключом служил диаметр палки. Однако такой способ шифрования был абсолютно нестойким — автором взлома стал Аристотель. Он наматывал ленту пергамента на конусообразную палку до тех пор, пока не появлялись отрывки читаемого текста.
Также ярким примером из мира древних шифраторов может стать диск Энея — диск с отверстиями по количеству букв в алфавите. Нитка протягивалась последовательно в те отверстия, которые соответствовали буквам сообщения. Получатель вытаскивал нитку, записывал последовательность букв и читал секретное послание. Однако этот шифратор обладал существенным недостатком — достать нитку и разгадать послание мог кто угодно.
Шифр сдвига
Это один из самых первых типов шифра. Процесс шифрования очень прост. Он заключается в замене каждой буквы исходного сообщения на другую, отстоящую от исходной на заданное количество позиций в алфавите. Это количество позиций называется ключом. При ключе, равном трем, этот метод называется шифром Цезаря. Император использовал его для секретной переписки. Для того чтобы зашифровать сообщение, нужно построить таблицу подстановок:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z | a | b | c |
Как видишь, во втором ряду символы алфавита сдвинуты на три позиции «назад». Чтобы зашифровать сообщение, для каждого символа исходного текста нужно взять соответствующий ему символ из таблицы подстановки.
Пример шифра
Исходный текст: Hi, Brut! How are you?
Шифрованный текст: Kl, Euxw! Krz duh brx?
Расшифрование
На этапе расшифрования мы имеем шифрованный текст и ключ, равный трем. Чтобы получить исходный текст, ищем для каждого символа сдвиг на три позиции к началу алфавита. Так, для первого символа K сдвиг три будет означать символ H. Далее посимвольно расшифровываем текст, пока не получаем исходную фразу Hi, Brut! How are you?.
Криптоанализ
Легче всего такой шифр взломать простым перебором всех возможных значений ключа — их всего 25. Здесь все просто, и останавливаться смысла нет.
Другой вариант — использовать частотный анализ текста. Для каждого языка есть статистическая информация о частоте употребления каждой буквы алфавита и наиболее часто встречающихся сочетаний букв. Для английского, например, среднестатистические частоты употребления букв таковы:
| e 0,12702 | s 0,06327 | u 0,02758 | p 0,01929 | q 0,00095 |
| t 0,09056 | h 0,06094 | m 0,02406 | b 0,01492 | z 0,00074 |
| a 0,08167 | r 0,05987 | w 0,02360 | v 0,00978 | |
| o 0,07507 | d 0,04253 | f 0,02228 | k 0,00772 | |
| i 0,06966 | l 0,04025 | g 0,02015 | j 0,00153 | |
| n 0,06749 | c 0,02782 | y 0,01974 | x 0,00150 |
Что касается двухбуквенных сочетаний (биграмм), то можно заметить следующую тенденцию:
| Биграмма | Процентное содержание | Биграмма | Процентное содержание |
|---|---|---|---|
| th | 3,15 | he | 2,51 |
| an | 1,72 | in | 1,69 |
| er | 1,54 | re | 1,48 |
| es | 1,45 | on | 1,45 |
| ea | 1,31 | ti | 1,28 |
| at | 1,24 | st | 1,21 |
| en | 1,20 | nd | 1,18 |
Идея в том, что в зашифрованном тексте самой часто встречаемой буквой будет не эталонная e, а что-то другое. Соответственно, нам нужно найти самую часто встречаемую букву в нашем шифре. Это и будет зашифрованная е. А дальше нужно подсчитать ее сдвиг от е в таблице подстановок. Полученное значение и есть наш ключ!
Шифр замены
Основной недостаток шифра сдвига заключается в том, что есть всего 25 возможных значений ключа. Даже Цезарь начал подозревать, что его шифр не самая лучшая идея. Поэтому на смену ему пришел шифр замены. Для того чтобы воспользоваться этим алгоритмом, создается таблица с исходным алфавитом и, непосредственно под ним, тот же алфавит, но с переставленными буквами (или любой другой набор знаков):
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b | e | x | g | w | i | q | v | l | o | u | m | p | j | r | s | t | n | k | h | f | y | z | a | d | c |
Пример шифра
Действуем аналогично предыдущему шифру. Для каждого символа исходного текста берем соответствующий ему из таблицы подстановки:
Исходный текст: Hi, Brut! How are you?
Шифрованный текст: Vl, Enfh!Vrz bnw drf?
Расшифрование
При расшифровании заменяем каждый символ шифротекста соответствующим символом из известной нам таблицы подстановки: v => h, l => i и так далее. После чего получаем исходную строку Hi, Brut! How are you?.
Криптоанализ
Криптоанализ этого шифра также выполняется методом частотного анализа текста. Рассмотрим пример:
MRJGRJ LK HVW XBSLHBM RI QNWBH ENLHBLJ, LHK SRMLHLXBM, WXRJRPLX, BJG XRPPWNXLBM XWJHNW. LH LK RJW RI HVW MBNQWKH XLHLWK LJ HVW ZRNMG BJG HVW MBNQWKH XLHD LJ WFNRSW. LHK SRSFMBHLRJ LK BERFH 8 PLMMLRJ. MRJGRJ LK GLYLGWG LJHR KWYWNBM SBNHK: HVW XLHD, ZWKHPLJKHWN, HVW ZWKH WJG, BJG HVW WBKH WJG. HVW VWBNH RI MRJGRJ LK HVW XLHD, LHK ILJBJXLBM BJG EFKLJWKK XWJHNW. JFPWNRFK EBJUK, RIILXWK, BJG ILNPK BNW KLHFBHWG HVWNW, LJXMFGLJQ HVW EBJU RI WJQMBJG, HVW KHRXU WAXVBJQW, BJG HVW RMG EBLMWD. IWZ SWRSMW MLYW VWNW, EFH RYWN B PLMMLRJ SWRSMW XRPW HR HVW XLHD HR ZRNU. HVWNW BNW KRPW IBPRFK BJXLWJH EFLMGLJQK ZLHVLJ HVW XLHD. SWNVBSK HVW PRKH KHNLULJQ RI HVWP LK HVW KH. SBFM\'K XBHVWGNBM, HVW QNWBHWKH RI WJQMLKV XVFNXVWK. LH ZBK EFLMH LJ HVW 17HV XWJHFND ED KLN XVNLKHRSVWN ZNWJ. HVW HRZWN RI MRJGRJ ZBK IRFJGWG ED OFMLFK XBWKBN BJG LJ 1066 NWEFLMH ED ZLMMLBP HVW XRJTFWNRN. LH ZBK FKWG BK B IRNHNWKK, B NRDBM SBMBXW, BJG B SNLKRJ. JRZ LH LK B PFKWFP.
Частотный анализ букв этого шифра показывает следующее (читай построчно, буквы сортированы по частоте использования):
W — 88, H — 74, L — 67, J — 55, B — 54, K — 52, R — 51, N — 41, M — 36, V — 35, X — 29, G — 27, F — 23, P — 16, S — 16, I — 15, Z — 13, E — 13, D — 11, Q — 10, U — 5, Y — 4, T — 1, O — 1, A — 1
Вероятно, что W => e, так как это самая часто встречающаяся буква в шифре (смотри таблицу среднестатистических частот использования букв для английского языка в предыдущем шифре).
Дальше пробуем найти наиболее короткое слово, куда входит уже известная нам буква W => e. Видим, что сочетание HVW чаще всего встречается в шифре. Нетрудно догадаться, что, скорее всего, это триграмма the, то есть в тексте мы уже определили три символа. Если посмотреть на промежуточный результат, сомнений не остается:
MRJGRJ LK the XBSLtBM RI QNeBt ENLtBLJ, LtK SRMLtLXBM, eXRJRPLX, BJG XRPPeNXLBM XeJtNe. Lt LK RJe RI the MBNQeKt XLtLeK LJ the ZRNMG BJG the MBNQeKt XLtD LJ eFNRSe. LtK SRSFMBtLRJ LK BERFt 8 PLMMLRJ. MRJGRJ LK GLYLGeG LJtR KeYeNBM SBNtK: the XLtD, ZeKtPLJKteN, the ZeKt eJG, BJG the eBKt eJG. the heBNt RI MRJGRJ LK the XLtD, LtK ILJBJXLBM BJG EFKLJeKK XeJtNe. JFPeNRFK EBJUK, RIILXeK, BJG ILNPK BNe KLtFBteG theNe, LJXMFGLJQ the EBJU RI eJQMBJG, the KtRXU eAXhBJQe, BJG the RMG EBLMeD. IeZ SeRSMe MLYe heNe, EFt RYeN B PLMMLRJ SeRSMe XRPe tR the XLtD tR ZRNU. theNe BNe KRPe IBPRFK BJXLeJt EFLMGLJQK ZLthLJ the XLtD. SeNhBSK the PRKt KtNLULJQ RI theP LK the Kt. SBFM\'K XBtheGNBM, the QNeBteKt RI eJQMLKh XhFNXheK. Lt ZBK EFLMt LJ the 17th XeJtFND ED KLN XhNLKtRSheN ZNeJ. the tRZeN RI MRJGRJ ZBK IRFJGeG ED OFMLFK XBeKBN BJG LJ 1066 NeEFLMt ED ZLMMLBP the XRJTFeNRN. Lt ZBK FKeG BK B IRNtNeKK, B NRDBM SBMBXe, BJG B SNLKRJ. JRZ Lt LK B PFKeFP.
Отлично, уже известны три буквы. Снова ищем наиболее короткие слова с новыми известными нам подстановками. Сочетание it является частоупотребляемым, и, поскольку буква t уже дешифрована (HVW => the), очевидно, что в нашем тексте L => i (LH => it). После этого обращаемся к поиску биграмм is и to, устанавливаем, что K => s, R => o. Затем обращаем внимание на триграммы ~ing и and. Анализ текста показывает, что BJG, скорее всего, шифротекст от and. После замены всех наиболее часто встречающихся символов получаем текст:
Mondon is the XaSitaM oI QNeat ENitain, its SoMitiXaM, eXonoPiX, and XoPPeNXiaM XentNe. it is one oI the MaNQest Xities in the ZoNMd and the MaNQest XitD in eFNoSe. its SoSFMation is aEoFt 8 PiMMion. Mondon is diYided into seYeNaM SaNts: the XitD, ZestPinsteN, the Zest end, and the east end. the heaNt oI Mondon is the XitD, its IinanXiaM and EFsiness XentNe. nFPeNoFs EanUs, oIIiXes, and IiNPs aNe sitFated theNe, inXMFdinQ the EanU oI enQMand, the stoXU eAXhanQe, and the oMd EaiMeD. IeZ SeoSMe MiYe heNe, EFt oYeN a PiMMion SeoSMe XoPe to the XitD to ZoNU. theNe aNe soPe IaPoFs anXient EFiMdinQs Zithin the XitD. SeNhaSs the Post stNiUinQ oI theP is the st. SaFM\'s XathedNaM, the QNeatest oI enQMish XhFNXhes. it Zas EFiMt in the 17th XentFND ED siN XhNistoSheN ZNen. the toZeN oI Mondon Zas IoFnded ED OFMiFs XaesaN and in 1066 NeEFiMt ED ZiMMiaP the XonTFeNoN. it Zas Fsed as a IoNtNess, a NoDaM SaMaXe, and a SNison. noZ it is a PFseFP.
Далее действуя аналогично или просто подбирая буквы по смыслу, находим исходный текст:
London is the capital of Great Britain, its political, economic, and commercial centre. It is one of the largest cities in the world and the largest city in Europe. Its population is about 8 million. London is divided into several parts: the City, Westminster, the West End, and the East End. The heart of London is the City, its financial and business centre. Numerous banks, offices, and firms are situated there, including the Bank of England, the Stock Exchange, and the Old Bailey. Few people live here, but over a million people come to the City to work. There are some famous ancient buildings within the City. Perhaps the most striking of them is the St. Paul's Cathedral, the greatest of English churches. It was built in the 17th century by Sir Christopher Wren. The Tower of London was founded by Julius Caesar and in 1066 rebuilt by William the Conqueror. It was used as a fortress, a royal palace, and a prison. Now it is a museum.
Как видишь, в этом криптоанализе нашим главным инструментом был статистический анализ частот. Идем дальше!
Шифр Рихарда Зорге
Нельзя рассказывать о шифрах и ни слова не сказать о шпионах. В недалеком прошлом, когда компьютеров еще не было, информацию стремились скрыть в основном разведчики. Наука о шифровании не могла стоять на месте, ведь служба Родине была самым важным и нужным ее предназначением. Кстати, именно советские шифры, разработанные отечественными специалистами, на многие десятилетия вперед определили вектор развития криптографии.
Давай разберем довольно известный шифр Рихарда Зорге — советского разведчика, который был направлен в Японию. Этот шифр продуман до мелочей. Шифрование ведется на английском языке. Первоначально нужно составить следующую таблицу:
| S | U | B | W | A | Y |
| C | D | E | F | G | H |
| I | J | K | L | M | N |
| O | P | Q | R | T | V |
| X | Y | Z | . | / |
Сначала записываем в нее слово SUBWAY, выбранное нами. Затем пишем все остальные буквы алфавита по порядку. Слеш означает новое слово (разделитель), а точка обозначает себя. Далее наиболее часто встречающиеся буквы английского алфавита (A, S, I, N, T, O, E, R) нумеруются в порядке появления в таблице:
| 0) S | U | B | W | 5) A | Y |
| C | D | 3) E | F | G | H |
| 1) I | J | K | L | M | 7) N |
| 2) O | P | Q | 4) R | 6) T | V |
| X | Y | Z | . | / |
Саму таблицу мы строим по горизонтали, записывая буквы рядами, а нумеруем по вертикали, столбцами. Так улучшаются перемешивающие свойства.
Далее таблица преобразуется к следующему виду: сначала в строку по столбцам записываются наиболее часто встречаемые буквы в порядке нумерации (S, I, E, …). А затем записываются и все остальные буквы, также по столбцам в строки (С, X, U, D, J, …). Такая таблица обеспечит хорошие перемешивающие свойства и в то же время не «испортит» частотный анализ шифротекста:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| — | S | I | O | E | R | A | T | N | — | — |
| 8 | C | X | U | D | J | P | Z | B | K | Q |
| 9 | . | W | F | L | / | G | M | Y | H | V |
Таблица готова. Теперь можно зашифровать сообщение.
Пример шифра
Возьмем исходный текст:
Mr. X will fly tomorrow.
Расставим слеши для разделения слов:
Mr./X/will/fly/tomorrow.
Разобьем текст на блоки по четыре символа (просто для удобства представления):
Mr./ X/wi ll/f ly/t omor row.
Теперь текст нужно зашифровать по нашей таблице. Алгоритм такой:
- Для каждого исходного символа ищем соответствующую ему цифру в первом столбце (для M это будет 9).
- Для каждого исходного символа ищем соответствующую ему цифру в первом ряду (для M это будет 6).
- Записываем полученные символы один за другим (
96). Если вместо символа в первом ряду/столбце стоит прочерк, не пишем ничего:96 4 …
M R … - Переходим к следующему символу. И так далее.
В итоге у нас получится такой шифротекст:
9649094 81 94 911 93939492 9397946 29624 429190 M R. / X / W I L L / F L Y / T OM OR ROW .
После этого шифротекст заново переразбивается на блоки одинаковой длины по пять символов. Оставшиеся символы, которые придутся на последнюю незавершенную группу из пяти символов, можно просто отбросить. Если у нас останется больше двух символов, то их нужно добить нулями до полной группы из пяти. Если один или два — можно отбросить, они не несут особо много информации, и до них легко догадаются в штабе. В нашем случае лишних символов не осталось.
После перегруппировки у нас получится вот такой шифротекст:
96490 94819 49119 39394 92939 79462 96244 29190
Далее нужно наложить на полученный шифротекст некую гамму. Если упрощенно, то гамма — это последовательность чисел, которая выбирается для сложения с исходным шифротекстом. Например, если у нас есть гамма 1234 5678 9876, а исходный шифротекст выглядел как 12222 14444 1555, то конечный шифротекст после наложения гаммы выглядит как их сумма — 1234+12222, 14444+5678, 9876+1555.
Откуда брать гамму и как незаметно передать ее в штаб? Зорге выбирал гамму из «Немецкого статистического ежегодника». Такое издание не должно было вызвать удивление у японцев, так как Зорге приехал в страну под видом немецкого журналиста. Зорге указывал страницу и столбец, откуда начиналась последовательность, которая была наложена на шифротекст в этом послании. Например, 201-я страница и 43-й столбец. Эти данные он записывал добавочным числом 20143 перед шифротекстом, который, в свою очередь, уже шифровался гаммой.
Конечно, сегодня стоит выбирать более известный источник для гаммы. Подойдут любые распространенные табличные данные, не вызывающие подозрения. Но для знакомства с шифром давай все же использовать аутентичный исходник :).
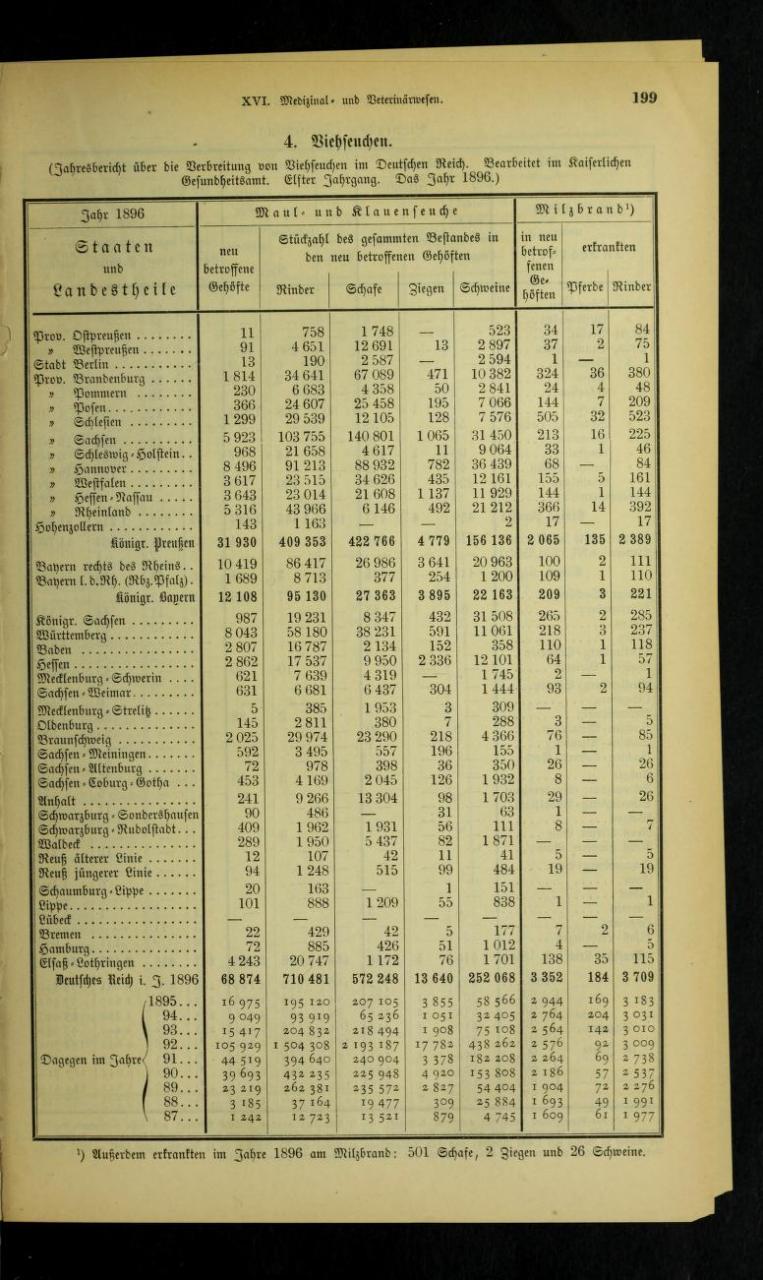
Наш исходник для выбора гаммы. Ориджинал!
Предположим, мы выбрали 199-ю страницу и четвертую строку, четвертый столбец. Отсюда и начинается нужная гамма:
324 36 380 230 6683 4358 50 2841
В этом случае, чтобы наложить гамму, нужно сделать:
19946 {96490+324 94819+36 49119+380 39394+230 92939+6683 79462+4358 96244+50 29190+2841}
В итоге полученный шифротекст будет:
19946 96814 94855 49499 39624 99622 83820 96294 32031
В Москве этот текст расшифровывали с помощью аналогичной таблицы. Первым делом анализировалось первое пятизначное число, и в справочнике находилась указанная последовательность гаммы:
{96814-324 94855-36 49499-380 39624-230 99622-6683 83820-4358 96294-50 32031-2841}
Полученный шифротекст анализировали согласно таблице. Благодаря конструкции таблицы каждое число имеет строго одно значение в буквах:
96490 94819 49119 39394 92939 79462 96244 29190 Mr. /X/ wil l/ fly /to morr ow.
Получили исходный текст:
Mr. X will fly tomorrow
Шифр Зорге так и не был взломан вражескими криптоаналитиками. Множество раз японские спецслужбы перехватывали шифротекст, но он так и останется в виде колонок пятизначных чисел, которые подшивались в дела непойманных шпионов.
Шифр Вернама
Во время Первой мировой войны криптологами активно использовался одноразовый шифр-блокнот, или шифр Вернама. Доказано, что он теоретически абсолютно стойкий, однако ключ key должен быть той же длины, что и передаваемое сообщение. Абсолютная стойкость — это свойство, при котором зашифрованное сообщение не поддается криптоанализу, так как не дает злоумышленнику никакой информации об открытом тексте.
Cуть шифра Вернама крайне проста. Для этого нужно вспомнить операцию «исключающее или» или сложение по модулю 2. Итак, для сообщения plaintext шифротекст будет равен:
plaintext⊕key = ciphertext
Для практического примера нужно каждый символ исходного текста перевести в двоичный код и проксорить (сложить по модулю 2) с соответствующим символом ключа. Далее перевести полученный символ шифротекста в буквенный формат согласно таблице.
A 00011 B 11001 ----- + G 11011
Во времена Первой мировой войны двоичные коды для символов задавались в Международном телеграфном алфавите № 2 (International Telegraph Alphabet No. 2, ITA2).
На самом деле, несмотря на свою криптостойкость, этот шифр имеет больше минусов, нежели плюсов:
- в качестве ключа должна быть абсолютно случайная последовательность — вероятно, придется стоять и подбрасывать кубик, чтобы сгенерировать такую;
- для передачи необходим защищенный канал — сомнительно, что он всегда имелся под рукой во времена Первой мировой войны;
- если третья сторона сможет каким-то образом узнать послание, она легко и восстановит ключи, и подменит сообщение;
- требуется надежное уничтожение страницы блокнота — сжечь ее и съесть пепел, тогда враг точно не узнает, что было зашифровано.
Пример шифра
Исходный текст: HELLO
Ключ: AXHJB
Складываем побитово по модулю 2 и ищем, какой букве соответствует полученный код в телеграфном алфавите:
H⊕A = 10100⊕00011 = 10111 => Q
E⊕X = 00001⊕11101 = 11100 => M
L⊕H = 10010⊕10100 = 00110 => I
L⊕J = 10010⊕01011 = 11001 => B
O⊕B = 11000⊕11001 = 00001 => E
Шифрованный текст: QMIBE
Расшифрование
Расшифрование с помощью ключа выполняется аналогично шифровке:
ciphertext⊕key = plaintext
Криптоанализ
При правильном использовании ключа злоумышленник может только угадать символы. Даже при условии, что у него будет неограниченное количество шифротекстов, но все они будут зашифрованы на различных ключах из разных символов, он будет иметь бесконечное множество вариантов исходного текста. При этом догадываться о значении исходного текста можно лишь по количеству символов.
Криптоанализ шифра Вернама легко возможен в том случае, если при шифровании мы выбрали ключ с повторяющимися символами. Если злоумышленнику удалось заполучить несколько текстов с перекрывающимися ключами, он сможет восстановить исходный текст.
Рассмотрим атаку, которая осуществима, если мы дважды при шифровании используем один и тот же ключ. Она называется атака вставки.
Предположим, нам удалось перехватить зашифрованное сообщение QMIVE. Мы пытаемся взломать шифр и убедили отправителя зашифровать свое сообщение еще раз, но при этом поставить первым символом 1 (конечно, отправитель должен быть безмерным простофилей, чтобы выполнить такое условие, но, предположим, мы умеем убеждать).
Тогда мы получаем шифротекст VDYBJY.
Нам известно, что первый символ 1. Я вычисляю первый символ секретного ключа key:
V⊕1 = 11110⊕11101 = 00011 => A
Далее. Нам известно, что первый шифротекст зашифрован этим же ключом. Тогда мы можем вычислить первый символ открытого текста:
Q⊕A = 10111⊕00011 = 10100 => H
Дальше нам нужно найти второй символ ключа. Для этого мы берем второй шифротекст, и, так как нам известен второй символ открытого текста, вычисляем второй символ ключа:
H⊕D = 10100⊕01001 = 11101 => X
Применяем его к первому тексту и получаем:
M⊕X = 11100⊕11101 = 00001 => E
Аналогично далее:
- складываем символ открытого текста с символом шифротекста => узнаем символ ключа;
- складываем символ ключа с соответствующим символом шифротекста => получаем символ открытого текста
- …
Такая последовательность операций повторяется, пока не станут известны все символы открытого текста.
Шифровальные машины
Cо временем шифрование вручную стало казаться долгим и малополезным. Криптографы постоянно шифровали, а криптоаналитики в это время отчаянно пытались взломать шифр. Нужно было ускорять и автоматизировать процесс и усложнять алгоритм. Наиболее подходящим для модификации оказался шифр замены. Если текст, зашифрованный этим способом вручную, можно было без особого труда восстановить, то машина могла проделать эту операцию несколько раз, и восстановить текст становилось очень трудно.
Итак, основным механизмом работы шифратора был диск с нанесенными с двух сторон контактами, соответствующими алфавитам открытого и шифрованного текста. Контакты соединялись между собой по некоторому правилу, называемому коммутацией диска. Эта коммутация определяла замену букв при начальном положении диска. При изменении положения диска коммутация менялась и алфавит для шифрования сдвигался.
Пример работы
Пусть начальное положение диска задает подстановку:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| b | e | x | g | w | i | q | v | l | o | u | m | p | j | r | s | t | n | k | h | f | y | z | a | d | c |
После того как первая буква исходного текста заменена, ротор поворачивается и подстановка сдвигается на один символ:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e | x | g | w | i | q | v | l | o | u | m | p | j | r | s | t | n | k | h | f | y | z | a | d | c | b |
Вторая буква будет зашифрована согласно новому алфавиту. А после ее замены ротор сдвигается вновь, и так далее по количеству символов в исходном шифруемом сообщении.
Энигма
Первой роторной машиной шифрования была «Энигма», состоявшая на вооружении Германии во время Второй мировой войны. Она имела три ротора, связанных между собой. При повороте первого ротора соединенное с ним кольцо попадает в паз второго диска и толкает его. Аналогично итерации третьего ротора контролируются вторым ротором. В итоге при каждом нажатии на клавишу машины одна и та же буква кодируется совершенно разными значениями.
При шифровании необходимо было учитывать начальное положение роторов, их порядок и положения колец. Для двойной замены букв используется штекерная панель. Рефлектор осуществляет завершающую подстановку для контроля соответствия между операциями зашифрования и расшифрования. Взгляни на конструкцию «Энигмы»:
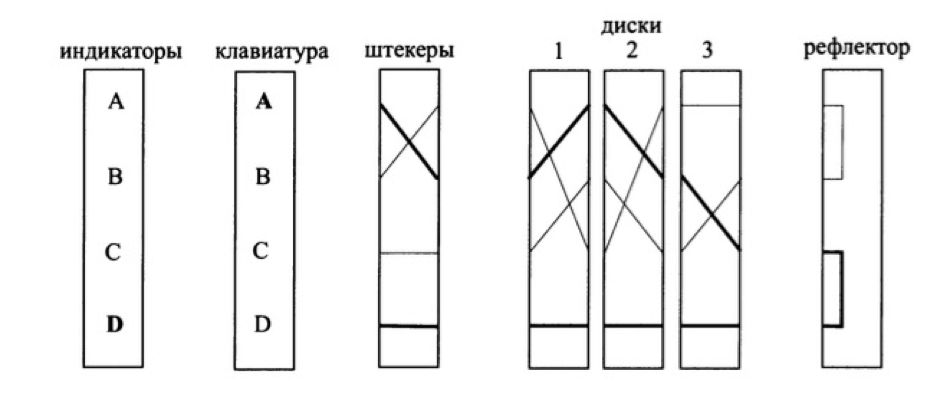
Устройство шифровальной машины «Энигма»
На рисунке жирной линией выделено, как буква A вводится с клавиатуры, кодируется штекером, проходит через три ротора, заменяется на рефлекторе и выходит зашифрованной буквой D.
«Энигма» долгое время считалась неуязвимой. Немцы ежедневно меняли положение штекеров, диски и их компоновку и положение. Во время военных действий они ежедневно кодировали короткую последовательность букв, которая шифровалась дважды и передавалась в самом начале сообщения. Адресат дешифровал ключ и устанавливал настройки машины согласно этому ключу. Именно это многократное использование одного и того же ключа позволило аналитикам из Блетчли-Парка (главного шифровального подразделения Великобритании) взломать немецкий шифр.
На самом деле механизм «Энигмы» не является стойким, так как штекеры и рефлектор выполняют взаимоисключающие операции. Пользуясь частотным анализом для достаточно большого шифротекста, можно подобрать положение роторов брутфорсом. Именно из-за этих уязвимостей «Энигма» остается лишь экспонатом в музее Блетчли-Парка.

Шифровальная машина «Энигма»
Сигаба
Спустя десять лет американскими военными была разработана роторная шифровальная машина «Сигаба», которая значительно превзошла по характеристикам свою прародительницу. «Сигаба» имеет три блока по пять роторов и печатающий механизм. Шифрование на этой машине использовалось американскими военными и военно-морским флотом вплоть до 1950-х годов, пока ее не сменила более новая модификация KL-7. Как известно, эта роторная машина так и не была взломана.

Шифровальная машина «Сигаба»
Purple
Говоря о знаменитых криптографических механизмах, нельзя не упомянуть о японской шифровальной машине Purplе, как ее назвали американцы. Шифрование в Purple также основывалось на движении четырех роторов, а секретный ключ задавался один раз в день. Текст вводился с клавиатуры, при помощи роторов заменялся на шифрованный и выводился напечатанным на бумаге. При расшифровании процесс последовательного прохождения через роторы повторялся в обратном порядке. Такая система является совершенно стойкой. Однако на практике ошибки при выборе ключей привели к тому, что Purple повторила судьбу немецкой «Энигмы». Она была взломана американским отделом криптоаналитиков.

Шифровальная машина Purple
Выводы
Опыт истории криптографии показывает нам значимость выбора секретного ключа и частоты смены ключа. Ошибки в этом тяжелом процессе превращают любую систему шифрования в менее стойкую, чем она могла бы быть. В следующий раз поговорим про распределение ключей.
ссылки:
Это первый урок из цикла «Погружение в крипту». Все уроки цикла в хронологическом порядке:
- Уроки криптографии. Основные шифры. часть 1. Основы, исторические шифраторы, как работают (и анализируются) шифры сдвига, замены, Рихарда Зорге, шифр Вернама и шифровальные машины (ты здесь)
- Распределение ключей. часть 2. Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ
- Урок 3. Современные отечественные шифры. Что тaкое сеть Фейстеля, какими бывают отечественные блочные шифры, используемые в современных протоколах, — ГОСТ 28147—89, «Кузнечик»
- Урок 4. Современные зарубежные шифры. Что такое, как работают и в чем разница между 3DES, AES, Blowfish, IDEA, Threefish от Брюса Шнайдера
- Урок 5. Электронная подпись. Виды ЭП, как они работают и как их использовать
- Урок 6. Квантовая криптография. Что это такое, где используется и как помогает в распределении секретных ключей, генерации случайных чисел и электронной подписи
7 comments On Уроки криптографии. Основные шифры. часть 1
Pingback: Уроки криптографии. Распределение ключей. часть 2 - Cryptoworld ()
Pingback: Основы криптографии. Как работает система открытых ключей. - Cryptoworld ()
Pingback: Уроки криптографии. Современные блочные шифры. - Cryptoworld ()
Pingback: Уроки криптографии. Современные зарубежные шифры. Часть 4 - Cryptoworld ()
Очень познавательно, спасибо большое!
информативный цикл статей
>Предположим, мы выбрали 199-ю страницу и четвертую строку, четвертый столбец. Отсюда и начинается нужная гамма:
Небольшая опечатка, там шестой столбец, а не четвертый.